[コンプリート！] 多項式 分数 通分 364291

解 解1 ① t u e t2 u2 ② t u3 t e5 u15 ③ t u e t2 u2 ④ 10 e5 f4 f2 ⑤ 18 6 f15 e2 6 解2 ① t 63 t2 ② t 67 t12 ③ t 69 t ④ t 68 t7 ⑤ t 62 t3 ⑥ t部分分数分解というのは、次のように式を簡単にすることを言います。 \ \frac{7x13}{x^22x3} \xrightarrow{\text{部分分数分解}} \frac{2}{x3} \frac{5}{x1} \ もう少し正確な言い方だと 「ある有理式を多項式と分子の次数が分母の次数より小さい有理式 の和で表すこと」 となります。分数の分母、分子に多項式がある時は、いつも（括弧）があると考えます。 分数－分数 と見て、通分します。分母は2と3だから、 6に揃えます 分母は6に揃え、分子はまだ計算しません。 分子だけ計算します。問2の問題と同じようにできます。 最後に、分子の項が、両方とも同じ数で分母と

1章1節14 分数の多項式の計算は 中村 翔

多項式 分数 通分

多項式 分数 通分- 分数の通分のやり方を忘れてしまった方は、こちらで確認しておいてくださいね。 ★通分のやり方★分数の足し算・引き算の計算方法を解説！ 分子が多項式になっているときには、かっこをつけることが大事！ $$\frac{2a5}{2}\times 6$$ $$=\frac{(2a5)}{2}\times 6$$ $$=(2a5)\times 3$$ $$=6a15$$ かっこをつけ分母が違う帯分数の引き算では、通分してから計算をします。引き算をした後に、約分できるときは、忘れないようにしましょう。 ぴよ校長 さっそく解いてみよう！ 「分母が違う帯分数の引き算」問題集はこちら 下の問題画像や、リンク文字をクリックすると問題と答えがセットになったpdf

1章1節14 分数の多項式の計算は 中村 翔

この場合の計算手順は以下の通り。 分数の文字式の計算手順 通分する （）を外す 同類項でまとめて係数の足し算・引き算をする このときも後ろの分数の項の両方に「」がかかるのに気をつけましょう。 上のように丁寧に計算すれば間違いにくいです分数式の計算（通分する）一夜漬け高校数学214#一夜漬け #高校数学 #分数式 #通分分数の約分のやり方と教え方のコツ｜時間短縮に便利なテクニックを紹介 分数の約分は公倍数の単元と密接な繋がりがあります。 そのため公倍数が理解できていないと約分も理解できません。 逆に公倍数の単元が完璧に頭に入っているなら分数の約分も

 ここでの内容は、こんな人に向けて書いています 分数の計算が苦手 分数の足し算はできるけど、どうして通分するのか理由が分からない 通分するときとしないときの区別がつかない このページは、以下のような"分母が違う分数の足し算"の計算ができるようになることを目的としています部分分数分解はいろいろな分野で使う基本的な計算方法です！ 部分分数分解は，分数の和を計算するときに活躍します。 →分数で表された数列の和の問題と一般化 積分計算でも役立ちます。 →三角関数の有理式の積分 不等式の証明で役立つこともあり多項式を（デフォルトでは有理数の範囲で）因数分解する。 一変数多項式だけではなく、多変数多項式も因数分解する。 キーワード引数で deep=True とすると、通分の適用を与式の「内側」まで有効にする。 関数 apart と逆の働きをする。 モジュール sympypolyspartfrac ¶ 部分分数分解に関係

そこで，定積分を求めるときは，計算が最も楽になるように C=0 とする． ⇒ 定積分の計算では，原始関数の内で C=0 の場合を使う 1 多項式，分数関数，無理関数 不定積分の公式のまとめ α が実数で， −1 以外のとき ∫wn x α dx= xα1 α1nnn C (11) 課題1 を部分分数分解せよ。 通分による方法 ①定数A,Bを置く ②右辺を通分する。 ③左辺の分子と右辺の分子が恒等式になるよう、Aの値とBの値を決定する。 よって、 となる。 このようにして、定数を決め、通分して、通分した結果の分子が恒等式になる多項式を整数で割った分数どうしの加法・減法は、通分を行ってから同類項間の加減を行う。多項式の展開を行う際に、符号にはくれぐれも注意する。 平方根を含む分数では、平方根どうし、整数どうしはそれぞれ約分可能である。 分母に平方根がある場合、分母の平方根と同じものを分母

方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題

算数 分数を通分するときの最小公倍数を簡単に見つける方法を解説 数スタ

 (2)分数式は通分する 分数の前の符号がのとき、分子の符号に注意 (3)わり算（除法）は、分数にして約分 (4)分数のわり算は、横の文字を上にのせたあと、逆数にしてかける 3、「式の値」は、計算をしてから、代入する 式の計算を先に 代入するとき、多項式部分は積分される． 残るは有理式の積分である． これを計算すると となる． よって を得る． 例 6 61 (有理式関数の不定積分の具体例) (Type 6) , の場合の を求める． 例 6 62 (有理式の積分) (Type 5) 不定積分 を計算する． 被積分関数の有理式の分母が 0 分数関数とは、 ある変数についての分数式 の多項式であるとき、 \(\color{red なお、あらかじめ言っておくと 2 の 「通分 する」方法が一番オススメ です。 分母を払う方法は場合分けが必要ですし、グラフを書く方法は式が複雑だと手間になります。 それぞれの解き方を確認しま

1

2

 あなたは部分分数分解を単なる「式の変形」だと思い込んでいませんか？ 実は数学b の数列の単元や数学3の積分計算でとてもお世話になる、大切な式変形なんです。 今回は、その「部分分数分解」を、公式・やり方だけでなく数列の問題への応用を詳しく解説しました!式(多項式=polynomial)と分母より分子の次数が小さい分数式(真分数式＝proper fraction)の和(帯分数式 =mixed fraction)に直すことができることを意味します。 部分分数分解 また、真分数式と真分数式の和は通分しても真分数式になります。例で解説しましょう。 3次式無料ダウンロード・印刷できる小学5年生の算数プリント 分数の約分・通分を繰り返し練習できるプリントです。 分数の約分・通分（1） 答え 分数の約分・通分（2） 答え 分数の約分・通分（3） 答え 分数の約分・通分（4）

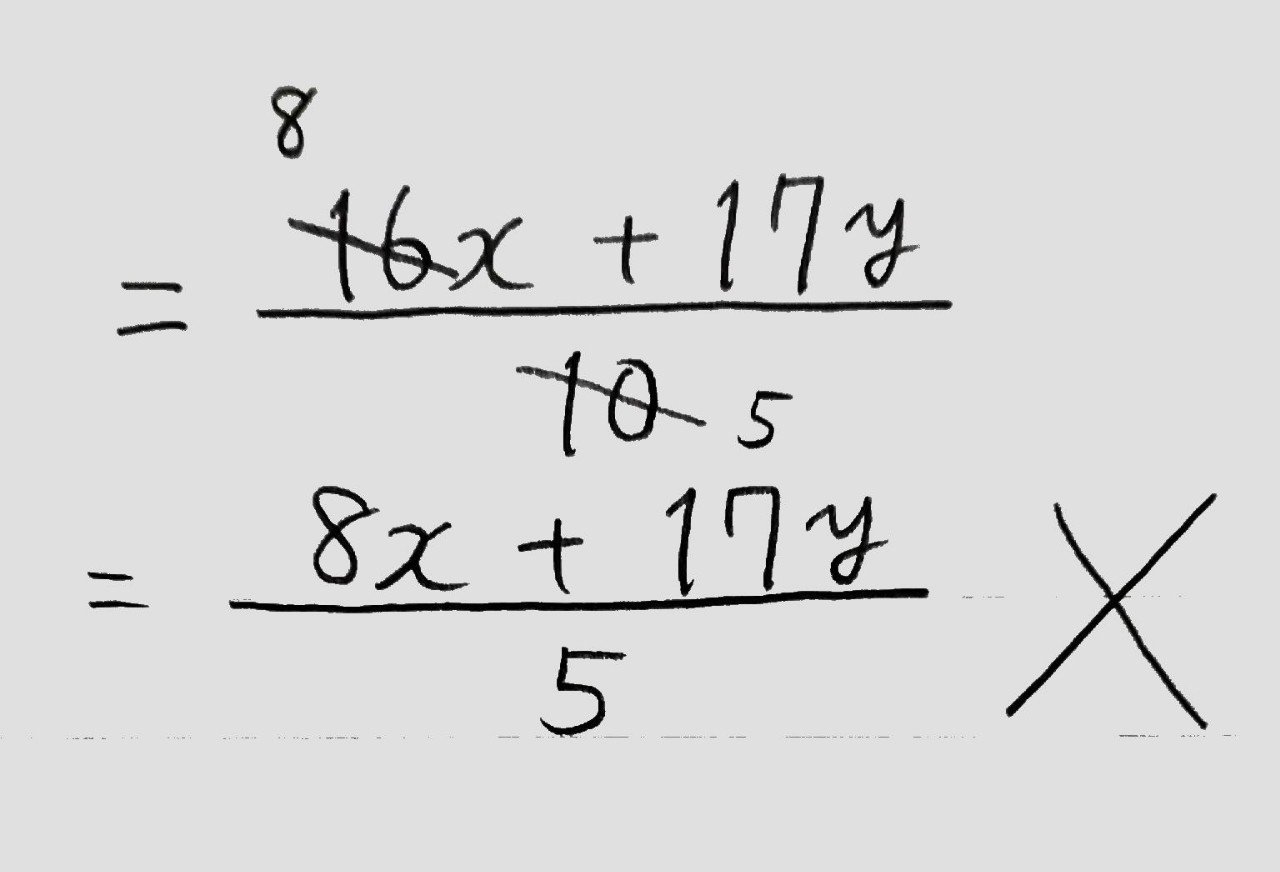
忙しい人のための中学数学 式の計算 計算ルール編 桜花 現役バイト塾講師 Note

多項式の掛け算 割り算と分配法則 代入計算のやり方 リョースケ大学

 分数の通分 だよね。 分数だけでヤッカイなのに、それが文字になる？！？ たまったもんじゃない笑 そこで今日は、 分数の文字式の通分方法 を3分で解説するよ。 通分がどうしてもできねえ！ってときに参考にしてみて^_^ 〜もくじ〜 そもそも通分って1分でわかる意味と定義、多項式との違い、次数、係数、分数との関係 有理式とは？1分でわかる意味、例、計算、分数式との関係 スポンサーリンク 分数式の約分、通分の計算 約分（やくぶん）とは、分数の分母と分子を同じ数で割り、できるだけ小さな数（簡単な数）にすることです代数学における部分分数分解（ぶぶんぶんすうぶんかい、英 partial fraction decomposition ）とは、有理式（あるいは分数式ともいう、多項式の商で表される式のこと）に対し、その有理式の分母が互いに素な多項式の積で表されるとき、その有理式を多項式と複数の有理式（ただし、分子の次数は

分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学

分数 文字式 約分

 式と証明｜分数式の加法や減法について 数学2 今回は、分数式の加法や減法について学習しましょう。 数だけの分数では一通り学習しているので、計算の流れを把握することはそれほど難しくありません。 大切なのは、分母や分子が整式となっ文字式の分数計算で困ったときには上で紹介したいずれかの方法で解けることが多いと思います。 困ったことがあれば、この記事を参考にしてもらえると嬉しいです^^ では、ポイントをおさらいしておきます。 分数の加減 分母を通分して揃えてから計算 通分がうまくわかりません X/416ーX/32=23/5 この式が通分すると 16x (16ーx)=128×23 となるようです。 しかし、16x (16ーx) となるのか、 128はどこからきたのか 分数を通分したのだろうけど、詳しくわからないので、自分で理解できず消化不良です

分母が違う分数の足し算 通分して計算する理由は分配法則を考えればわかる 数学の面白いこと 役に立つことをまとめたサイト

多項式の計算応用 分数をふくむ式 教遊者

 というわけで、今回の記事では中2で学習する 「多項式の計算」 についてイチから解き方を確認していきましょう。 かず先生 丁寧にやっていくから、苦手な人も最後までがんばろう！ スポンサーリンク Contents 1 多項式の計算のやり方 11 同類項を少数や分数を含んだ数式の展開にも対応しています。 約分の電卓 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。 通分の電卓 分数を通分できる電卓です。3つ以上の分数を通分する 多項式の計算について 多項式の計算について。 〇乗算 3(2x5y) = 3(2x)3(5y) = 6x15y 〇分配法則 分配法則とは、式中のパレンティス（丸括弧）の外の数字を中の項にそれぞれ掛けることです。 例：(a^22a3)*(5) = 5(a^2)5(2a)5(3) =5a^210a15 〇通分 通分とは、分数の加算や減算でお互いの分母を最小公

分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題

スタディピア 数と式

 式と証明｜繁分数式の計算について 今回は繁分数式の計算について学習しましょう。 高校では、数学だけでなく物理や化学などでも繁分数式を扱う機会が多くなります。 公式に代入する値が分数のときもあるからです。 繁分数式は、複雑な見た目をし多項式・有理式 多項式 とは、変数の整数次の多数の項で表される式のことである。 有理式とは、分数形式で表される式で分母と分子が多項式で表現されるものである。ゆえに多項式は、分母が1の時の有理式であると言うこともできる。ここでは、多項式の形式変換、分解、係数分離などを こうすることで、分数同士の通分を計算しなくて済みます。 やり方④割り算を含むとき 式の中に割り算（\(\div \ \)）が登場するときは、分数のかけ算（\(\times \ \displaystyle \frac{1}{ }\)）に変形しましょう。 そうすれば、問題なく分配法則を適用できます。

約分計算機 かんたん計算機

うさぎでもわかる解析 高校数学 数3 Part05 部分分数分解を用いた積分 工業大学生ももやまのうさぎ塾

問2 多項式では，各項の次数のうち，もっとも大きいものを，その多項式の次数といいます。 問 問3 分数をふくむ式でも同じように分配法則を使って計算できるよ。 係数の計算では，通分をして分母をそろえて計算しましょう！ いろいろな多項式の計算に挑戦しよう！ 2年 1章 式の計算4／7 p

分数の通分の意味とやり方 子どもに教える際のポイントやコツを解説 数学fun

通分のやり方 大人の学び直し算数 計算のやり方解説 無料

小学3年生 算数 無料問題集 分母が同じ分数の足し算 おかわりドリル

多項式の計算応用 分数をふくむ式 教遊者

分数の足し算や引き算の問題 通分できるかが非常に大切 中学や高校の数学の計算問題

Lh3 Googleusercontent Com Proxy Ql Ub D8m7ajmgv26v6bduqgp3yozb6ffuwamuck X 463dzn Lmwbpll7g173pnrdxbcmylceojk268pzooq7sp Fsqqxcpfj Upj9qqim4suo0w0a6offmm5ilw33afubp94 Rgdqkkzz265dywjtncp8jk0zs1rplptvvvinntnimmtvdc123z95raruuh3myywnbnoa1dmzjkj94daj Yght Ml8jpdqzlfdmir9fu5d Parwbvb0wvy9bqmj5t5 Hqec3kuacgdvilsz5hpozyb805ey Qqywedsxfedtqjhc5wz P4q2oecbcwpiyng7ep62iixhu906ki8puz5kr5srf9w7d 5mb4xzg0kk9j2ubzhgsdihkmv Uqcowr8e2uw8vqdxhspoey

約分 通分のポイント

中学数学 文字を用いた四則計算

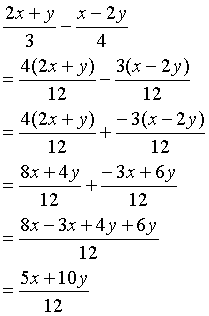
分数の復習と分数式の計算

分母が違う分数の足し算 通分して計算する理由は分配法則を考えればわかる 数学の面白いこと 役に立つことをまとめたサイト

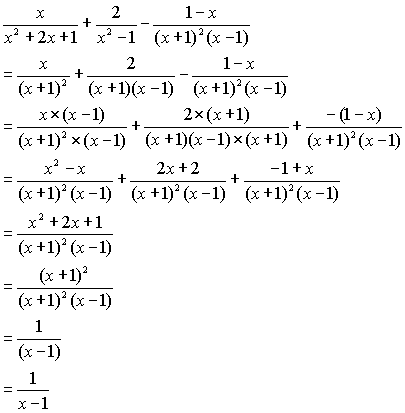
分数の復習と分数式の計算

分数の大小関係 通分や小数にするのが解き方のコツだ 中学や高校の数学の計算問題

たけのこ塾 Twitterren 中学数学 多項式の分数計算 のチェックテストです 解くためのポイント まず分子の部分にカッコをつける 分母が異なる場合は通分をする 方程式ではないので 分母を払わないよう注意 詳しくは画像の方をご覧下さい

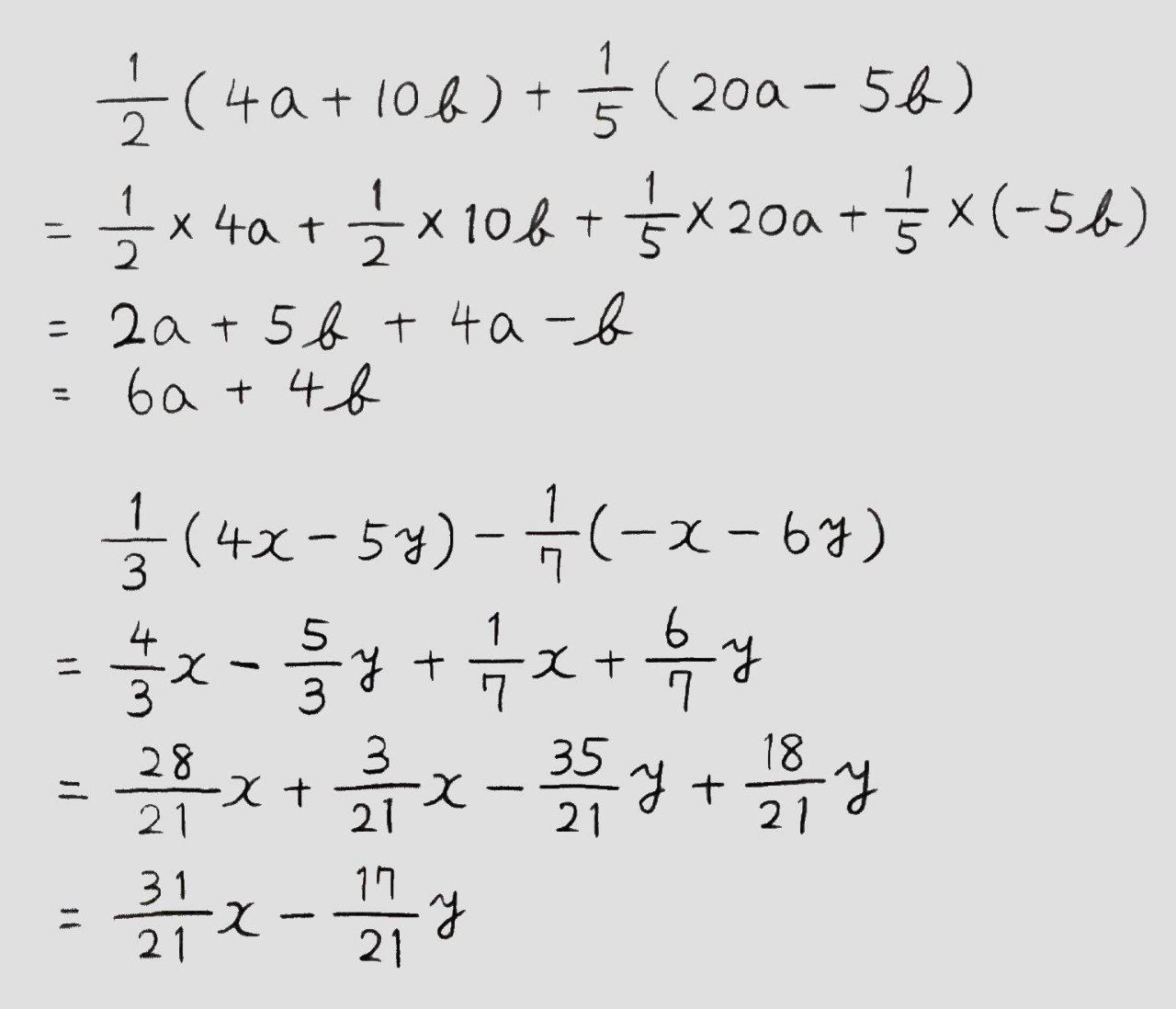
忙しい人のための中学数学 式の計算 計算ルール編 桜花 現役バイト塾講師 Note

通分と分母を払って計算する方法の使い分けを教えてください また Yahoo 知恵袋

分母の文字の払い方を教えて下さい 60 X 2 60 X えっくすまいなすに 中学校 教えて Goo

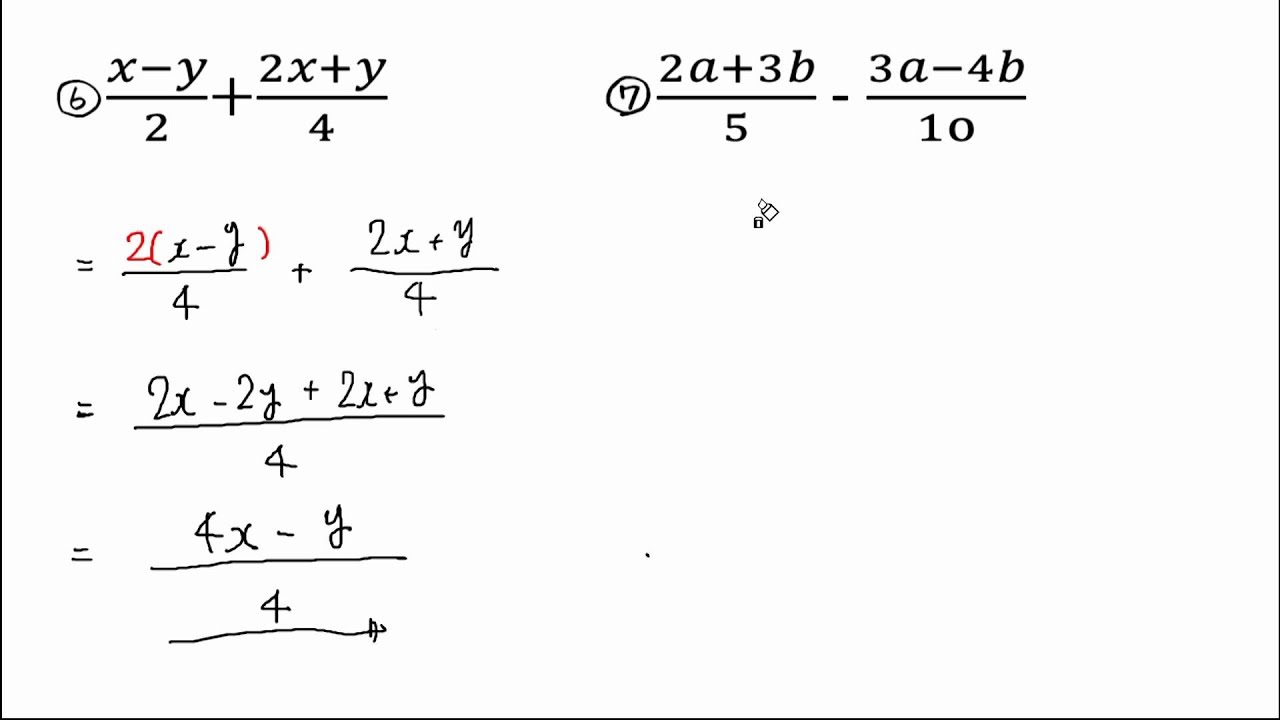
分数の入った文字式 Youtube

4 3 式の計算 通分のやつ 勉強できようサイト

小学5年生 算数 無料問題集 分母が違う帯分数の足し算 おかわりドリル

この分数の計算ですがまず通分するんですよね それとも最小公倍数を求めるんです Yahoo 知恵袋

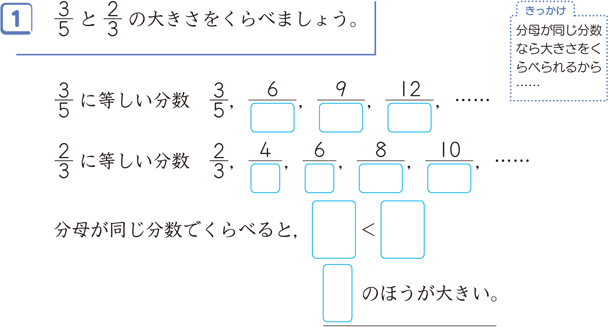
通分と約分 算数用語集

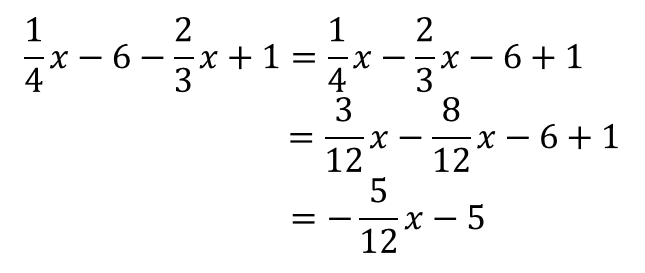
文字式 分数の計算問題を１から丁寧に 数スタ

多項式の分数の計算 数学２年 塾の先生が作った本当に欲しいプリント 楽天ブログ

分数を含む多項式を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに

分数がある式の計算 分数 中学生からの勉強質問 数学 進研ゼミ中学講座

分数の約分 分数 中学生からの勉強質問 数学 進研ゼミ中学講座

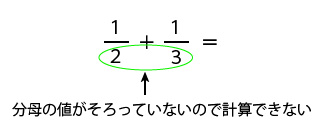
通分と約分 もう一度やり直しの算数 数学

文字式 分数の計算問題を１から丁寧に 数スタ

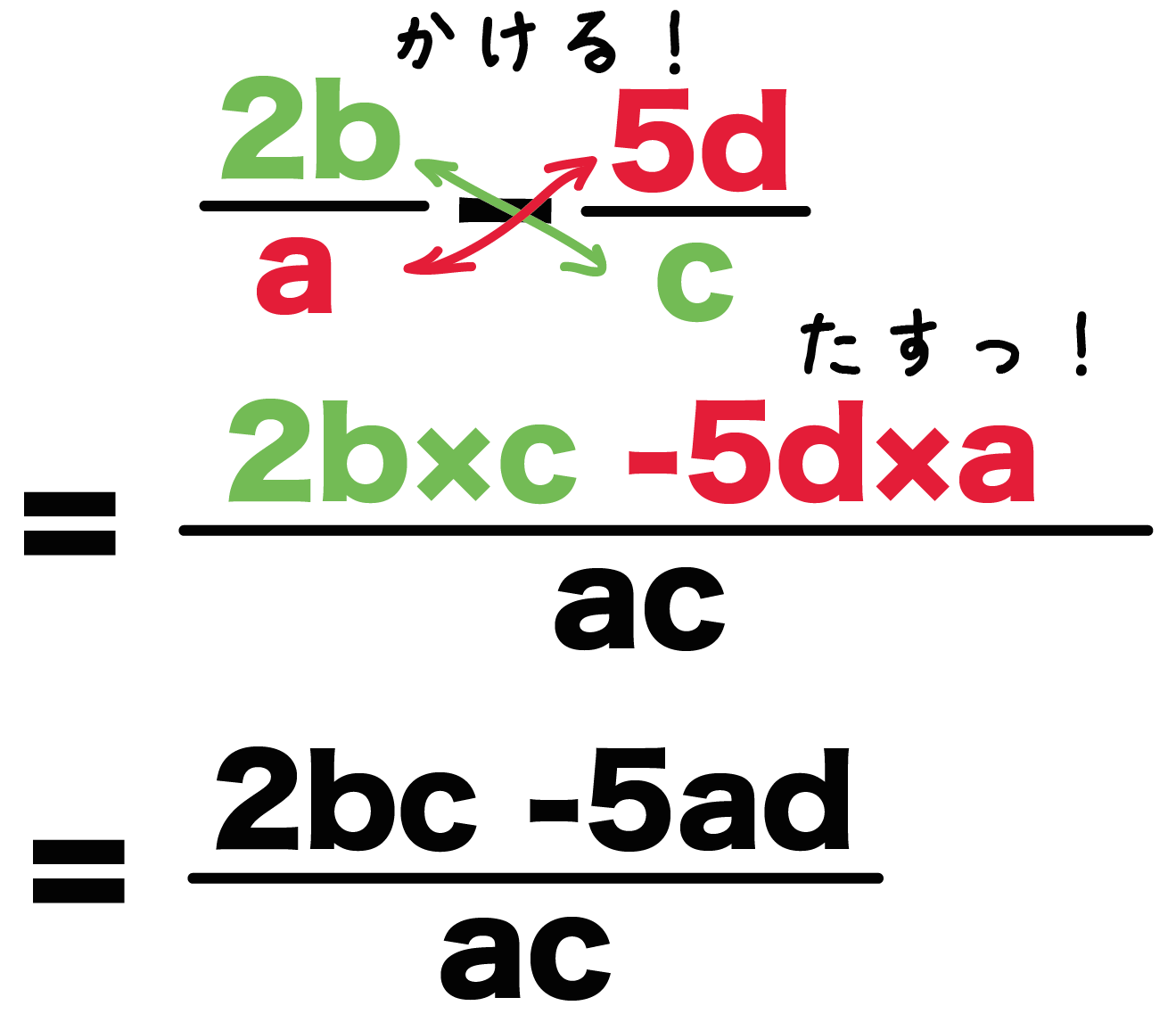
3分でわかる 分数の文字式の通分方法 Qikeru 学びを楽しくわかりやすく

文字が入った分数の足し算や引き算 分子にかっこをつけて通分する 中学や高校の数学の計算問題

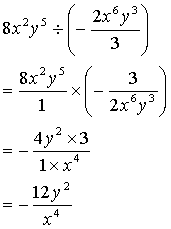
分数の復習と分数式の計算

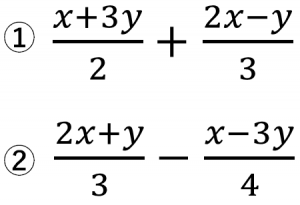
中2数学 式の計算 間違えやすい計算問題 4つのタイプ たけのこ塾 勉強が苦手な中学生のやる気をのばす

4で通分するのは 答えを見て分かったんですけど 8で通分しても 4で通分した Clearnote

1

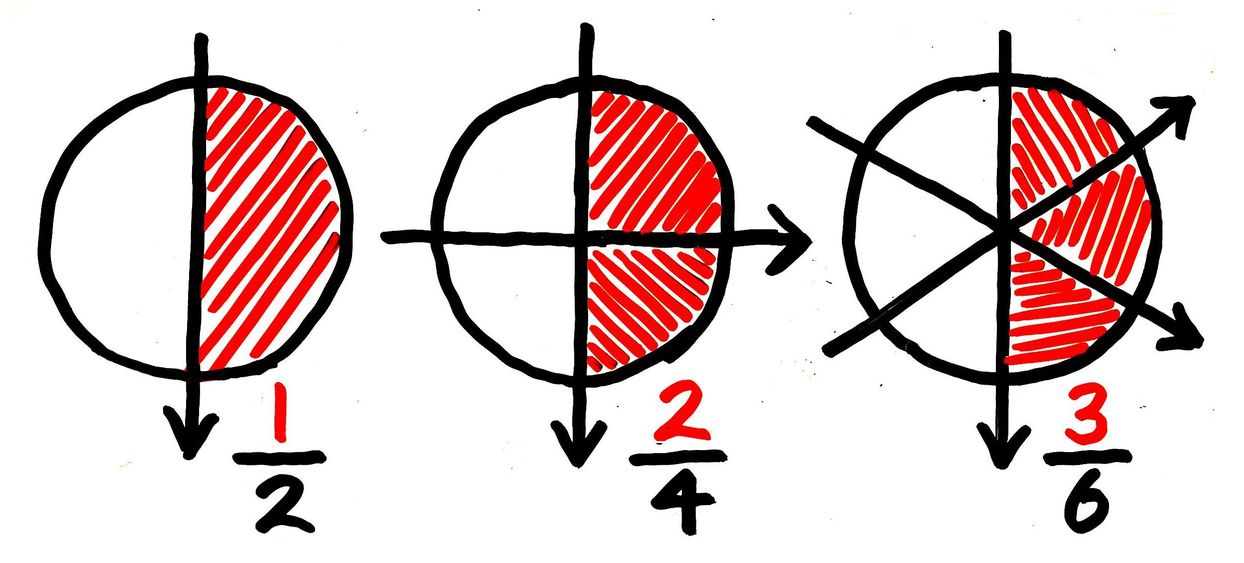
分数の約分のやり方とは 問題演習と既約分数も分かりやすく教えます そうちゃ式 分かりやすい図解算数 別館

1章1節14 分数の多項式の計算は 中村 翔

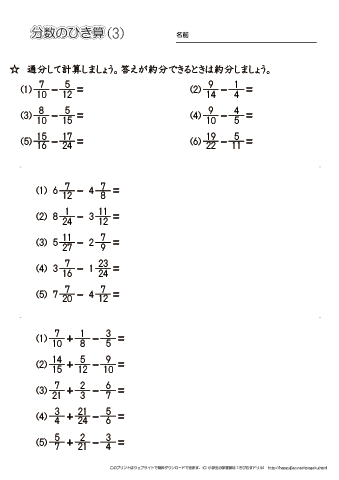
小学５年生の算数 異分母の分数の引き算 問題プリント ちびむすドリル 小学生

通分とは コトバンク

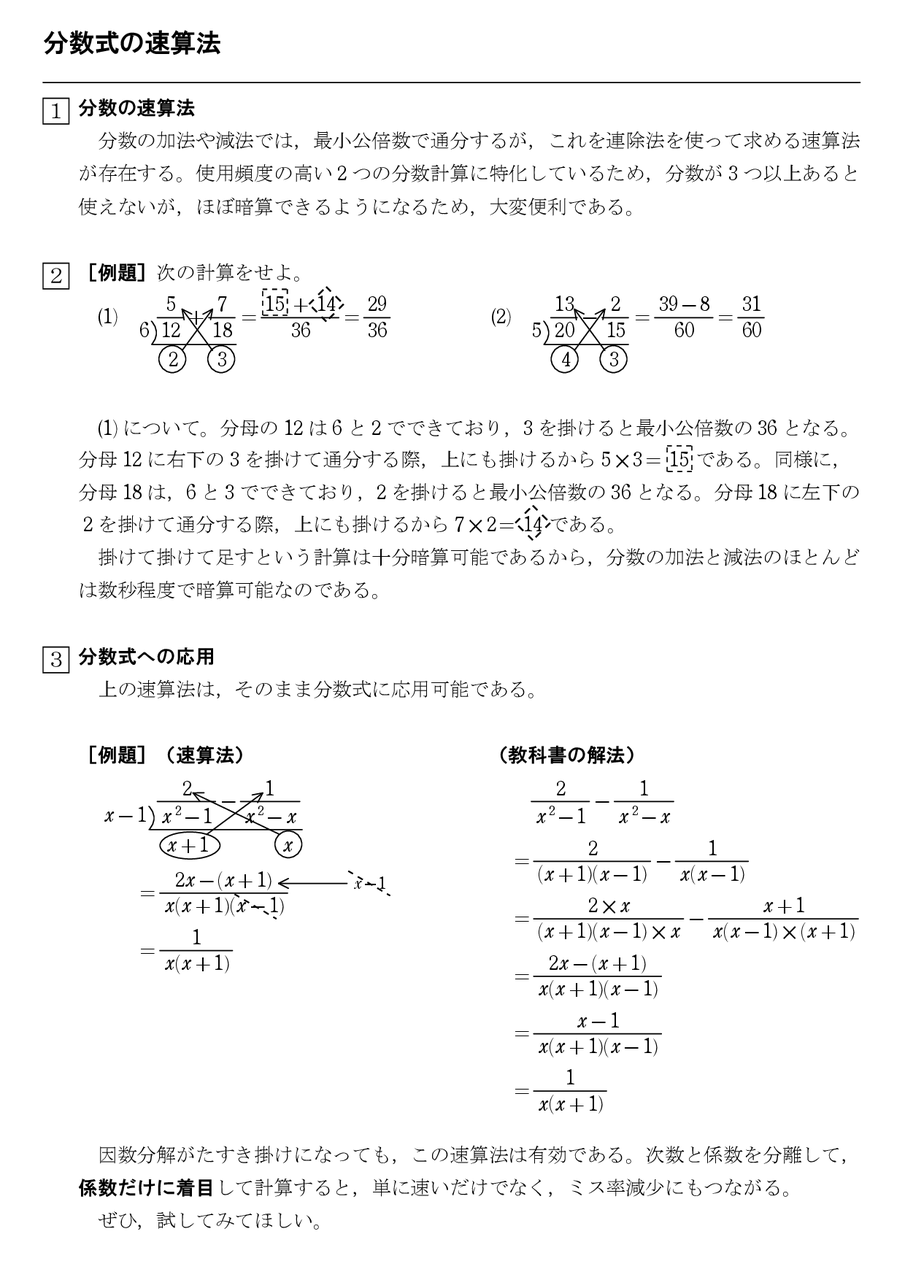
分数式の速算法１ 怜悧玲瓏 高校数学を天空から俯瞰する

分数式の基本的な計算と例 高校数学の美しい物語

いろいろな多項式の計算の分数をふくむ式の計算について質問がありま Yahoo 知恵袋

分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun

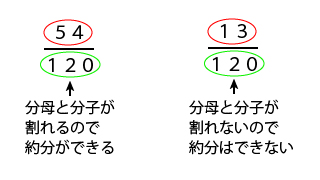
通分と約分 もう一度やり直しの算数 数学

中2 数学 1 6 多項式の計算 分数 Youtube

1

教えてください 分数の計算なので 分母が単項式ならそのまま通分 多項式な Yahoo 知恵袋

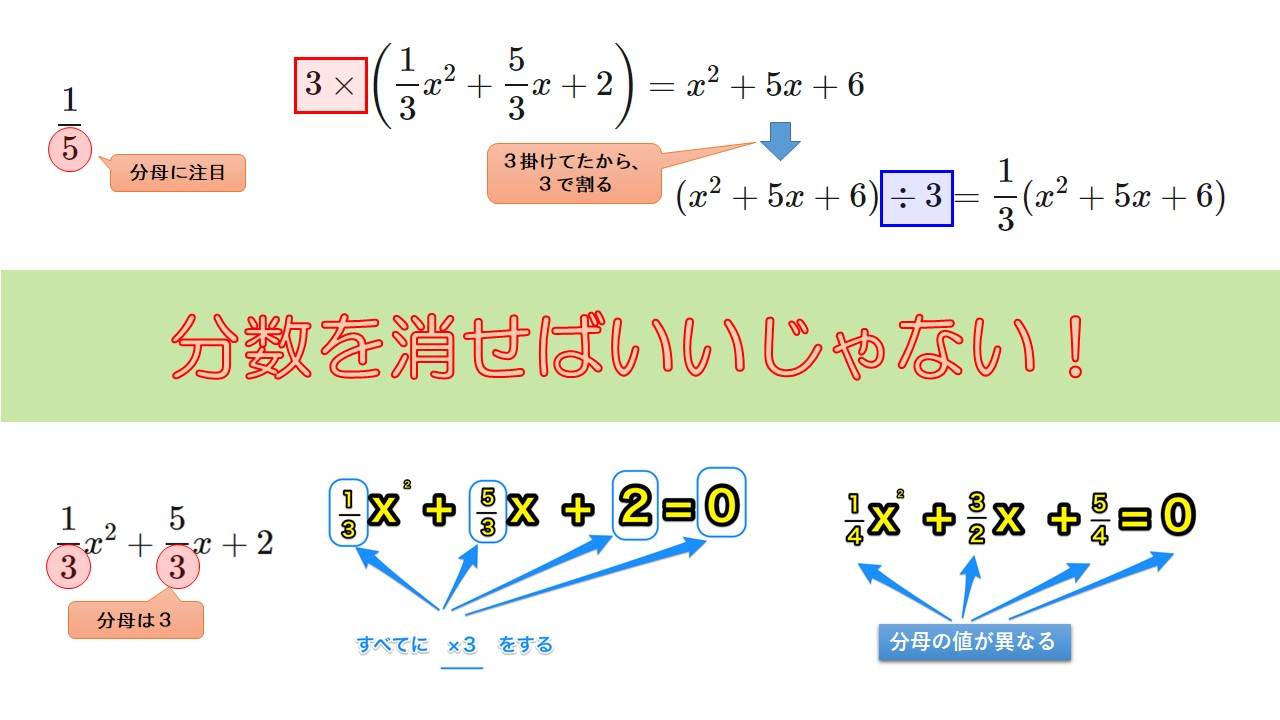
高校数学 因数分解 分数が登場する式を因数分解する方法 わかりやすく解説します 数学の面白いこと 役に立つことをまとめたサイト

部分分数分解の解法 通分をしないで済む ヘビサイドの目隠し法 あらきけいすけの雑記帳

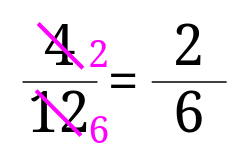
通分と約分の違いって何 なぜ分母と分子に同じ数を掛けたり割ったりできるの みけねこ小学校

くもんのにがてたいじドリル算数 7 小学5年生約分 通分をする分数の計算 本 通販 Amazon

高校数学 関数の極限 多項式関数と分数関数の極限 受験の月

通分のやり方 大人の学び直し算数 計算のやり方解説 無料

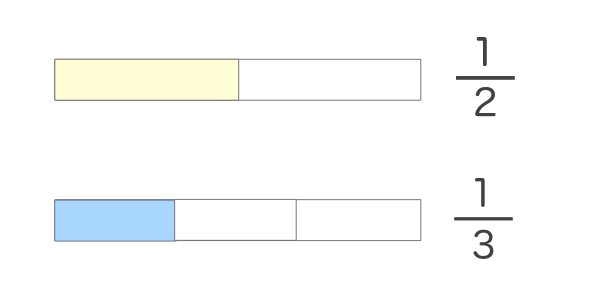
通分 簡単に計算できる電卓サイト

3分でわかる 分数の文字式の通分方法 Qikeru 学びを楽しくわかりやすく

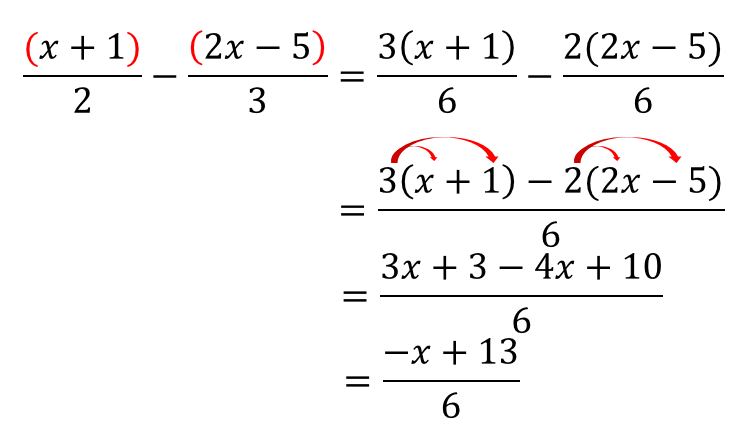
文字式 分数の計算問題を１から丁寧に 数スタ

分数の多項式の足し算や引き算 通分してからがポイントだ 中学や高校の数学の計算問題

通分のやり方 大人の学び直し算数 計算のやり方解説 無料

高校数学 分数式の加法と減法 映像授業のtry It トライイット

数 式と証明 分数式 通分 分母が因数分解できる場合 オンライン無料塾 ターンナップ Youtube

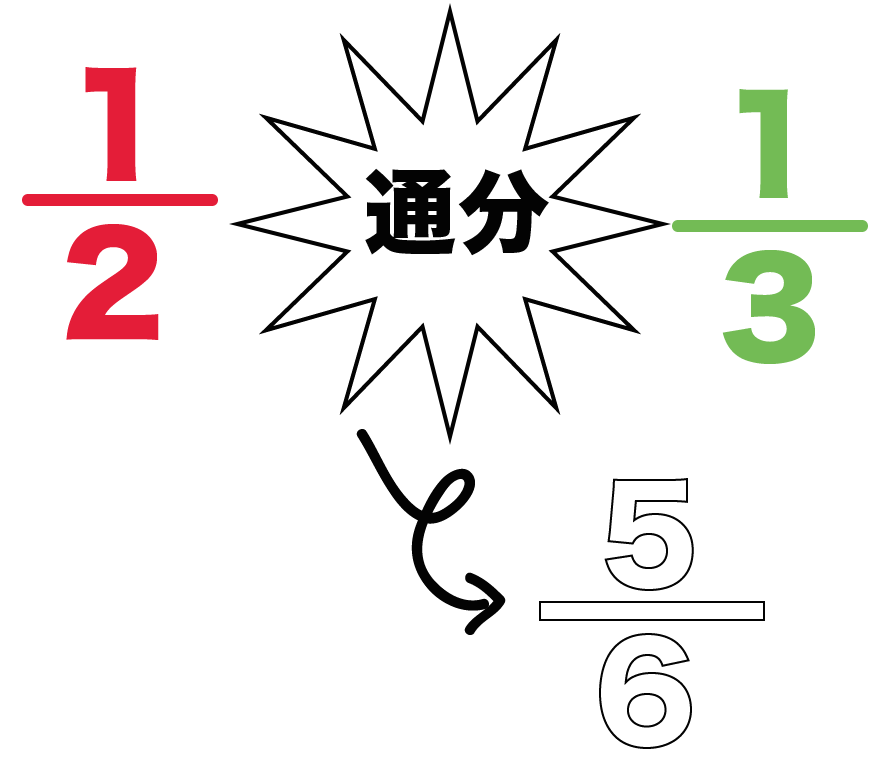
3分でわかる 分数の文字式の通分方法 Qikeru 学びを楽しくわかりやすく

小学5年生 算数 無料問題集 分母が違う分数の引き算 おかわりドリル

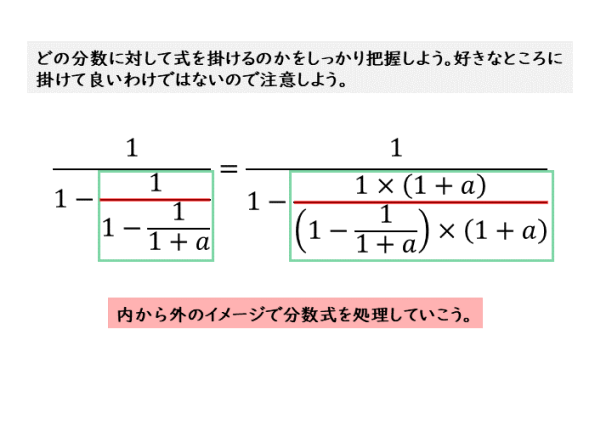
式と証明 繁分数式の計算について 日々是鍛錬 ひびこれたんれん

スタディピア 数と式

文字式の計算 分数の問題はどうやって解く やり方を解説するぞ 中学数学 理科の学習まとめサイト

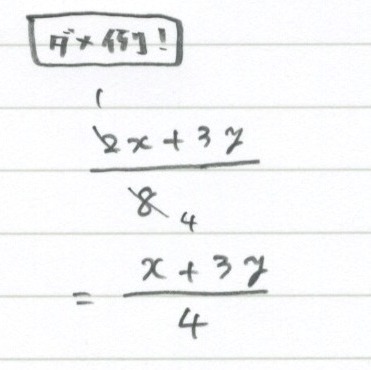
4 2 式の計算 約分の注意点 勉強できようサイト

通分のやり方 大人の学び直し算数 計算のやり方解説 無料

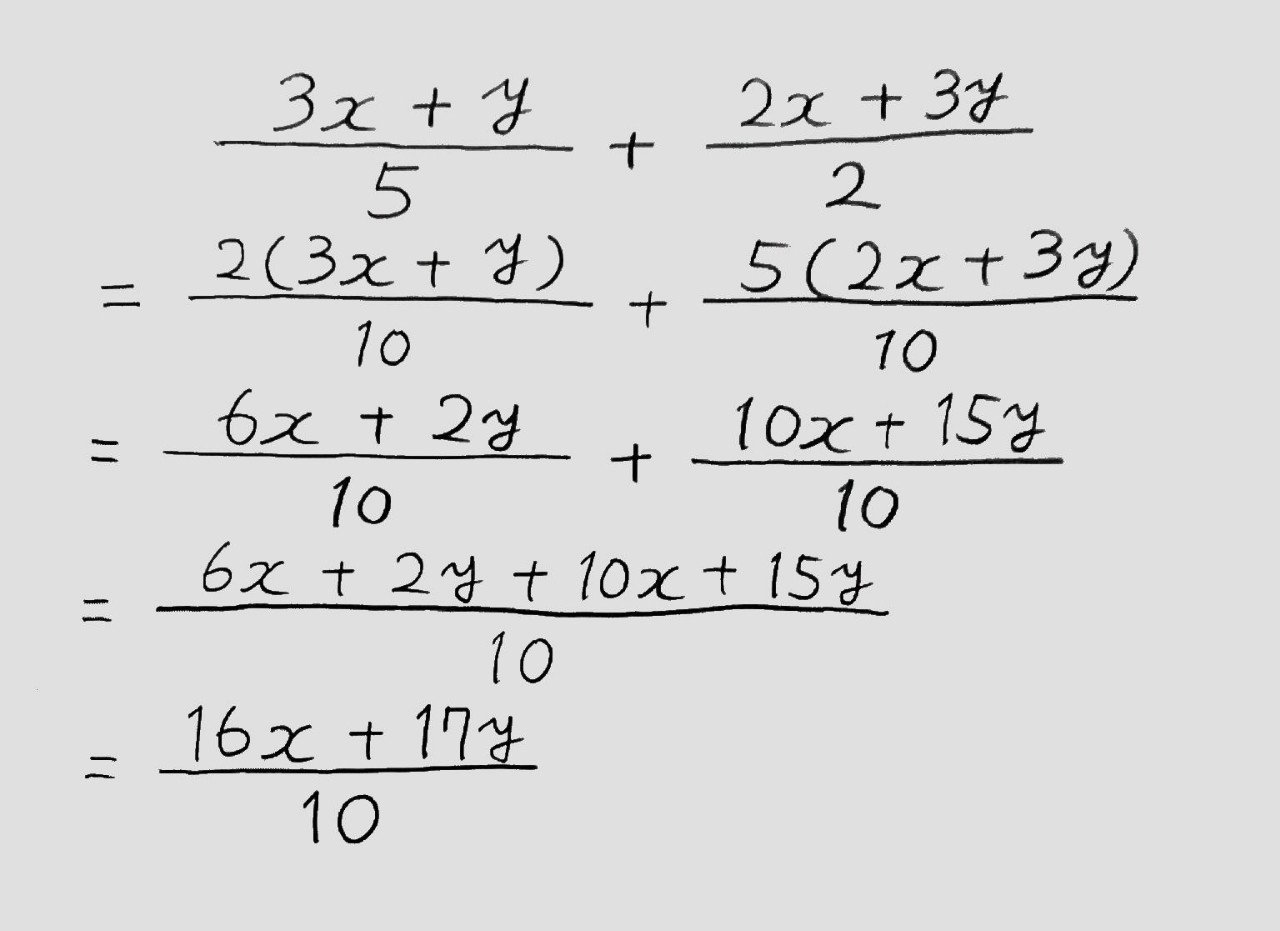
忙しい人のための中学数学 式の計算 計算ルール編 桜花 現役バイト塾講師 Note

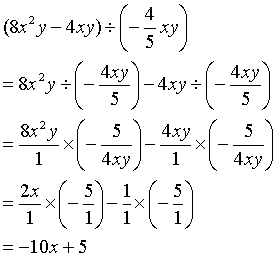
分数の復習と分数式の計算

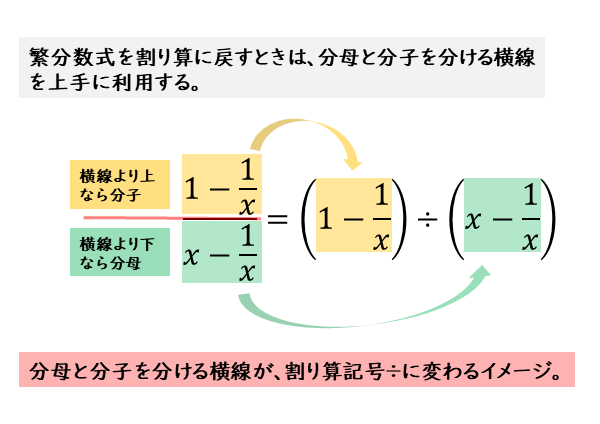
式と証明 繁分数式の計算について 日々是鍛錬 ひびこれたんれん

文字の入った分数の約分とマイナスの扱い 分数の文字式の計算 Youtube

文字式 カッコや分数を含んだ多項式 の計算方法 数学fun

文字式 カッコや分数を含んだ多項式 の計算方法 数学fun

数 式と証明 分数式 通分 分子が定数のもの オンライン無料塾 ターンナップ Youtube

多項式の計算 チーム エン

速算術 分数や分数式の足し算引き算を暗算で 高校生 数学のノート Clearnote

通分と約分 算数用語集

Suusenn Com

1

多項式の計算応用 分数をふくむ式 教遊者

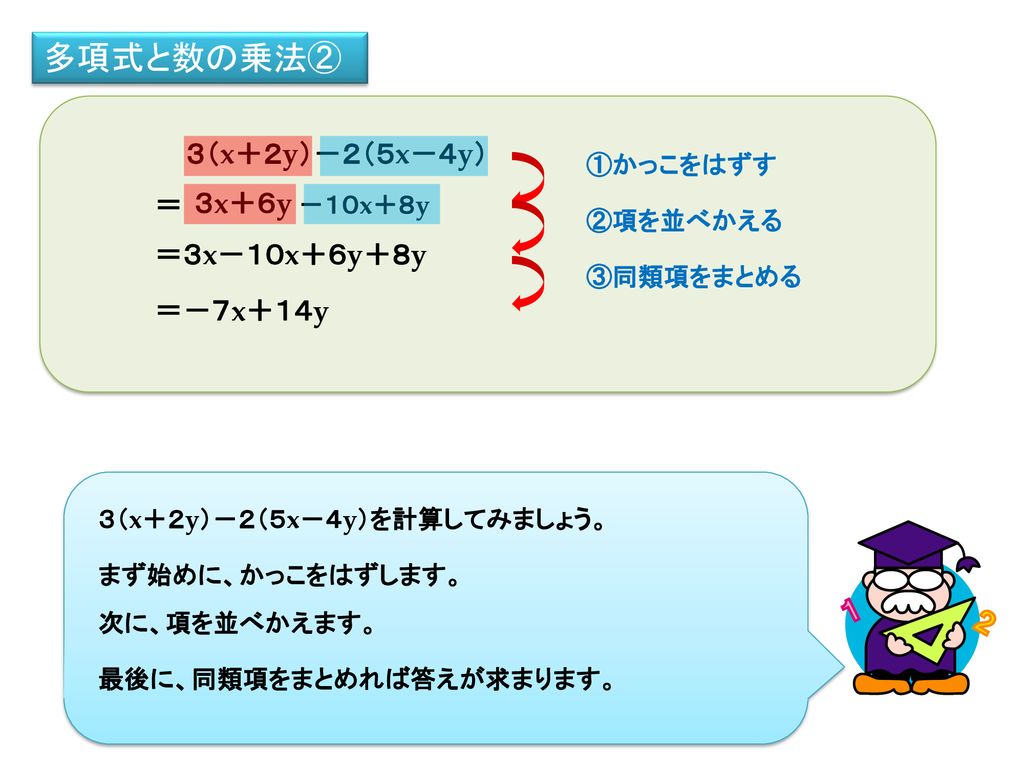
多項式と数の乗法 除法について学ぼう Ppt Download

文字式の分数の問題です 文字式の計算では分母をはらわず 通分する 数学 教えて Goo

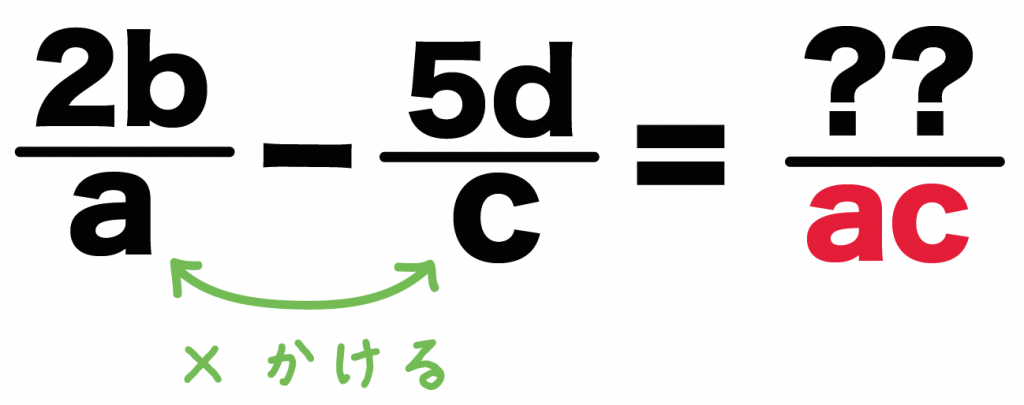
3分でわかる 分数の文字式の通分方法 Qikeru 学びを楽しくわかりやすく

小学５年生の算数 異分母の分数の引き算 問題プリント ちびむすドリル 小学生

3分でわかる 分数の文字式の通分方法 Qikeru 学びを楽しくわかりやすく

多項式の計算応用 分数をふくむ式 教遊者

通分と約分の違いって何 なぜ分母と分子に同じ数を掛けたり割ったりできるの みけねこ小学校

多項式の計算応用 分数をふくむ式 教遊者

中学数学2年 多項式の加法と減法 受験の月

文字式 カッコや分数を含んだ多項式 の計算方法 数学fun

分数 文字式 約分